Hier finden Sie momentan informelle Inhalte der Vorgängerversion dieser Website.
Berechnungen nach der Finite-Elemente-Methode helfen bereits in einem frühen
Stadium der Produktentwicklung bei der Analyse
Simulationen sind in vielen unterschiedlichen Branchen anwendbar und verbreitet. Sie sind dabei, technische Berechnungen - FEM in Ihrem Unternehmen einzusetzen? Sie suchen einen Dienstleister für kleine oder größere Berechnungsaufgaben?
Fragen Sie an!
Finite-Elemente in der Praxis
Anwendungen der Finite-Elemente-Methode finden als erprobte Technologie bei der Konzeption, Auslegung und
Validierung technischer Produkte regen Einsatz. Mittels FEM lassen sich physikalische Zusammenhänge auch in
komplexen Fällen realitätsnah simulieren. Die Simulation verlagert ein Bauteil in den Computer - bekannt als
"Digital Prototyping". Virtuelle Prototypen fördern vertiefte Einblicke in das Produktverhalten,
bringen Flexibilität für Bauteil- oder Machbarkeitsstudien und Variantenvielfalt und ermöglichen effiziente
Versuchbegleitungen.
Diese anspruchsvolle Methode führt zu langfristigem Erfolg, wenn der analysierende Ingenieur
die zu Grunde liegende numerische und physikalische Theorie beherrscht, die komplexe Software kennt, sie
beherrscht, zielgerichtet einsetzt und korrekte Schlussfolgerungen aus den Resultaten zieht.
Das Ingenieurbüro Schendel gewährleistet Ihnen eine zuverlässige, fachkundige und vertrauliche Durchführung von
Berechnungsdienstleistungen.

Die FEM ersetzt Ingenieurwissen nicht. Sie ist nur ein zusätzliches Hilfsmittel und darf nicht nach einem "Black Box" Prinzip im Vertrauen auf bunte Ergebnisgrafiken verwendet werden. Trotz weit entwickelter Rechentechnik und in Wissenschaft und Industrie erprobter Software: das Ergebnis kann nur so gut sein wie die Vorgaben des Ingenieurs. Know-how und Verantwortung des Anwenders liegen in der Modellfindung. Es ist abzuklären, wie stark man das Bauteil für die gestellte Aufgabe abstrahieren kann, z.B. durch Ausnutzung von Symmetrien oder Weglassen von unwesentlichen Details. Man muss sich Gedanken machen über die Wahl einer geeigneten Elementtechnologie, die Netzdichte, die richtige Zeitschrittwahl, die Approximation der Randbedingungen und Belastungen, die Wahl von realistischen Materialeigenschaften, mögliche Systemantworten (z.B. auftretende Nichtlinearitäten, Locking-Effekte, Hourglassing etc.), die Wahl eines geeigneten Gleichungslösers, die Beachtung des Aufwand-Nutzen-Verhältnisses (Rechenzeit/Kosten vs. Genauigkeit) sowie über die Verifizierung, Validierung und Interpretation der Ergebnisse. Die Software ist und wird zwar immer anwenderfreundlicher und ausgefeilter, für zuverlässige Ergebnisse ist aber das Wissen des Ingenieurs gefordert, eher mehr noch als früher.
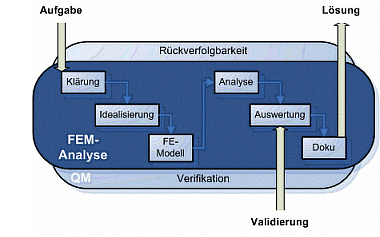
Die Finite-Elemente-Methode bietet zusammen mit modernen Algorithmen der Struktur- optimierung eine Plattform für eine wirtschaftliche Bauteilauslegung. Ziele des Einsatzes von Optimierungsmethoden sind z.B.
Um die Produktentwicklung zu beschleunigen und zu verbessern werden Optimierungs- module
eingesetzt. Diese unterstützen den Konstrukteur in der Gestaltfindung eines Bauteils.
In Zusammenarbeit können
Optimierungslösungen produktiv in laufende Entwicklungs- projekte
eingebunden werden. Durch den zielgerichteten Einsatz der Strukturoptimierung lässt sich Verbesserungs- und Einsparpotential
aufdecken.
Bei der Topologieoptimierung wird ausgehend von einem definierten Bauraum bzw. dem bestehenden Bauteil
und den vorhandenen Lagerungs- und Lastverhältnissen ein FE-Modell erstellt. In mehreren Schritten wird aus diesem
Ausgangsmodell eine am Optimum liegende Struktur hinsichtlich Steifigkeit, Massenverteilung und Materialverbrauch ermittelt.
Veranschaulichend ist das Prinzip der Topologieoptimierung dem biomechanischem Prinzip des Knochenwachstums nachempfunden:
"Fresszellen" bauen innerhalb der Knochen Gewebe an wenig belasteten Stellen ab, an stark belasteten Gebieten wird neues
Gewebe angelagert. Das Material richtet sich entlang des Kraftflusses aus. Technische Ziele sind die Ermittlung einer maximalen
Steifigkeit bei minimalem Gewicht, minimiertes Volumen oder eine veränderte Verteilung von Massen und Steifigkeiten, um
Resonanzen zu beeinflussen. Um brauchbare Ergebnisse zu erzielen, lassen sich
Fertigungsrestriktionen z.B. für Guss, Stanzbarkeit, Dichtigkeit oder Anforderungen an symmetrische Bauteilauslegung berücksichtigen.

Bei einem "konventionellen" Entwicklungsprozess wird in jeder Stufe der Entwicklung eine Ermittlung der Beanspruchungen durchgeführt
und das Ergebnis in die nächste Stufe eingebracht. Das Vorgehen bei der Topologieoptimierung liefert vertiefte Einblicke. Vorgaben für den Entwicklungsprozess
sind die gewünschten Eigenschaften und die Rand- bedingungen. Bereits zu Beginn werden die wesentlichen Anforderungen an die
strukturelle Auslegung eingegrenzt.
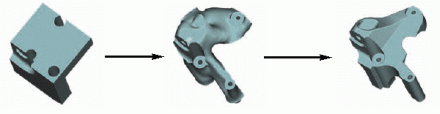
Mit der Shape- oder auch Formoptimierung werden am zu optimierenden
Bauteil relativ geringe Modifikationen an der Oberflächenform vorgenommen.
Ziel ist, Spannungs- konzentrationen zu homogenisieren und zu minimieren. Abgeleitet
vom Prinzip des voll beanspruchten Bauteils (FSD - "Fully Stressed Design")
nach einer Hypothese von NEUBER: eine optimale Form eines Bauteils ist dann erreicht,
wenn die Beanspruchungen längs der gefährdeten Oberflächenzone völlig konstant verlaufen. Zusätzlich nutzt man das
Abklinggesetz von NEUBER. Dieses Gesetz besagt veranschaulichend: eine bereichsweise Erhöhung der Spannungen kann zur Erhaltung
des statischen Gleichgewichtes in einem benachbarten Bereich eine Erniedrigung der Beanspruchung zur Folge haben
("entlastende Kerbwirkung"). Die Reduzierung der Spannungsspitzen und Homogenisierung der Spannungsverteilung wirkt sich
tragfähigkeitserhöhend und unter zyklischer Beanspruchung positiv auf die Lebensdauer aus.
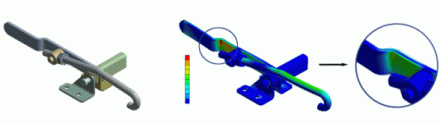
Zur Versteifung von dünnen, flächenartigen Strukturen werden häufig Erhöhungen oder Vertiefungen eingebracht.
Diese so genannten Versickungen führen mechanisch gesehen zu einer Erhöhung des Flächenträgheitsmoments. Sicken wirken hauptsächlich für Biegebeanspruchungen senkrecht zur Schale versteifend.
Durch Sickenoptimierung kann auch für komplexe Bauteilgeometrien die Form und
die Lage der Sicken (Sickenmuster) vorgeschlagen werden.
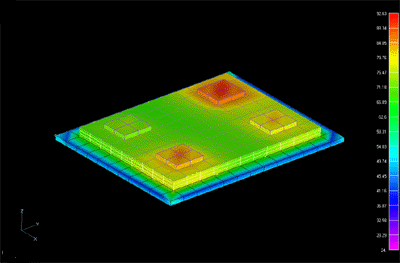
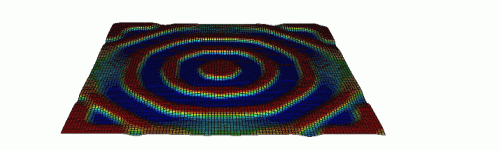 Bild: hinsichtlich Biegesteifigkeit optimierte Sickenanordnung eines gelenkig gelagerten Blechs unter mittiger Belastung. Sickenbilder
lassen sich auch für komplexe Geometrien ermitteln.
Bild: hinsichtlich Biegesteifigkeit optimierte Sickenanordnung eines gelenkig gelagerten Blechs unter mittiger Belastung. Sickenbilder
lassen sich auch für komplexe Geometrien ermitteln.
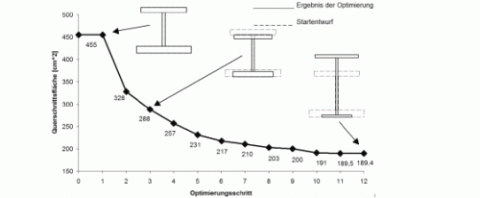
Bei der vielseitigen Parameter- oder Designoptimierung handelt es sich um die Verbesserung eines vorgegebenen
Konstruktionsentwurfes (Startlösung). Nach einem Suchalgorithmus wird durch mehrmaliges Lösen der normalen FEM-Aufgabe
ein gewünschter Zustand angestrebt. Die veränderbaren Eigenschaften des Bauteils werden dabei durch
Parameter beschrieben. Diese Variablen werden unter festgelegten Restriktionen adaptiv angepasst, um einen für den
Entwurf relevanten Wert systematisch zu verbessern. Klassische Optimierungsgrößen sind bei der Designoptimierung zum
Beispiel Maschinenteilgröße, Oberflächen, Volumen, Spannungen, Temperaturen usw. Allgemein ist eine beliebige Größe, die
in der FEM-Software durch eine Variable dargestellt werden kann, eine mögliche Zielfunktion der Optimierung.
Beim 3D-Druck im Fused Deposition Modeling Verfahren (FDM) wird verflüssigter Kunststoff durch Extrudieren
mit einer in der Fertigungsebene frei verfahrbaren Heizdüse entsprechend den zugrundeliegenden CAD-Daten aufgetragen.
Nach anschließendem Abkühlen erstarrt das Material zum realen Modell. Mögliche Vorteile des Einsatzes von Rapid
Prototyping Methoden sind
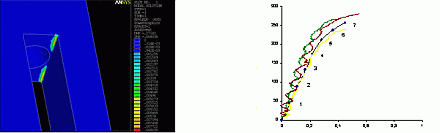
Statische strukturmechanische Untersuchungen sind eine der häufigsten Anwendungen der Finite-Elemente-Methode. Der Begriff Struktur umfasst z.B. Komponenten und Bauteile des Schiffbaus, der Luft- und Raumfahrt, des Metall-, Leicht- oder Glasbaus, des Bauwesens, der Automobilindustrie, der Medizintechnik oder der Konsumgüterindustrie: Maschinenelemente, Kolben, Werkzeuge, Brücken, Gebäude, Sport- und Freizeitgeräte und viele viele andere.
Bei diesen Analysen werden die Kräfte und Verformungen, die Dehnungen und mechanischen Spannungen in Strukturen berechnet, die auf vorwiegend ruhende Lasten zurückzuführen sind, also keine signifikanten Dämpfungs- oder Trägheitseffekte beinhalten.
Sowohl lineare als auch nichtlineare statische Analysen werden durchgeführt. Letztere sind immer dann erforderlich, wenn sich eine Struktur in nicht vernachlässigbarem Ausmaß nicht proportional zur Belastung verhält. Zu den Nichtlinearitäten, die berücksichtigt werden können gehören z.B. Material, Vorspannung, nichtkonservative Kräfte, große Verformungen, finite Strain oder Kontakt zwischen Bauteilen.
Bei den dynamischen Strukturanalysen können zusätzlich auch Trägheitskräfte und Dämpfungseffekte berücksichtigt werden.
Die Modalanalyse zählt zu den grundlegenden dynamischen Untersuchungen. Die interessierenden strukturellen Eigenschaften sind die Eigenfrequenzen und die Eigenschwingungsformen ("Modes"). Diese Modellparameter beschreiben das Schwingungs- verhalten und sind hinsichtlich der Abschätzung möglicher Resonanzanfälligkeit sowie für die Evaluation potentieller Beruhigungsmaßnahmen (z.B. Einbau von Schwingungstilgern, Steifigkeits- und Massenmodifikationen an der Struktur etc.) von großer Bedeutung.
Weiterhin können zeit- oder frequenzabhängige Belastungen und deren Auswirkungen auf die Struktur untersucht werden. Alle statischen Lastarten können dynamisch aufgebracht werden: erzwungene Beschleunigung, zeitverzögerte und zeitlich beschränkte Lasten, Zeitfunktionen, jede Last oder erzwungene Bewegung kann unterschiedliches zeitabhängiges Verhalten aufweisen. Unterschiedliche Arten von Dämpfung sowie Nichtlinearitäten lassen sich berücksichtigen.
Ziel einer Frequenzganganalyse ist es, die stationäre Antwort einer Struktur für verschiedene Anregungsfrequenzen zu berechnen und von Antwortgrößen (z.B. Verschiebungen) eine Kurve über die Frequenz zu erhalten (Harmonic Response). Dabei wird von Lasten ausgegangen, die über einen langen Zeitraum mit konstanter Amplitude und Frequenz einwirken. Anhand des Frequenzganges können "Antwortspitzen" der Struktur festgestellt und ausgewertet werden.
Die Antwortspektrum-Analyse wird eingesetzt, um Nachweise für komplexe Strukturen zu führen, die einer relativ lang anhaltenden, aber nicht andauernden transienten Belastung ausgesetzt sind. Beispiele hierfür sind Erdbebenbelastungen, Windlasten, Belastung durch Meereswellen usw. Dabei wird eine konservative Abschätzung für die maximale Beanspruchung in einer Struktur ermittelt. Dies erreicht man durch eine Überlagerung aller modalen Extrema für ein gegebenes Antwortspektrum, auf eine Rechnung im Zeitbereich wird verzichtet.
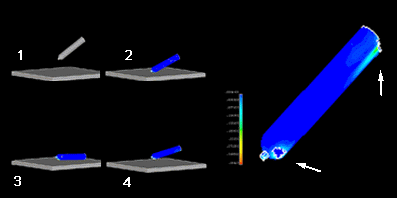
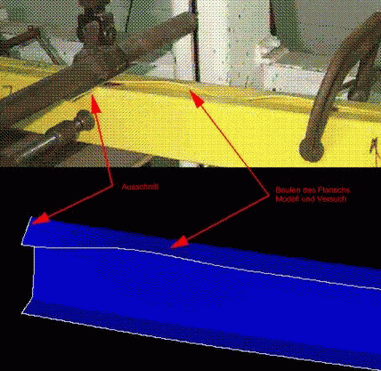
Bei einer Stabilitätsuntersuchung eines Bauteils geht es um die Frage, bei welchem Grenzwert der Belastung die Gleichgewichtslage der Struktur nicht mehr eindeutig ("stabil") bleibt und dadurch generell die Funktionstüchtigkeit des Bauteils gefährdet ist. Insbesondere bei schlanken Strukturen ist eine Untersuchung der Stabilität erforderlich, um Funktions- störungen oder Schadensfälle im Gebrauchszustand auszuschliessen. Knicken eines Fachwerkstabes, Kippen eines Trägers, Beulen bei Flächentragwerken oder Durchschlag- phänomene gehören zu dieser Kategorie des Bauteilversagens.
Nähert sich beispielsweise die Drucklast eines Stabes einem Grenzwert, der sog. Knicklast, so besteht die Gefahr, dass der Stab sich sichtbar durchzubiegen beginnt. Solche Punkte auf der Last-Verschiebungskurve nennt man auch Instabilitätspunkte. Die Struktur kann keine zusätzlichen Lasten mehr aufnehmen oder kollabiert durch eintretenden Steifigkeitsverlust.
Die Beurteilung der Stabilität eines Gleichgewichtszustandes für eine "perfekte" Struktur kann als Eigenwertproblem formuliert werden, die zugehörigen Eigenvektoren entsprechen der Knick- oder Beulform, in die die Struktur nach Verlust der Stabilität übergehen will (Versagensmodus). Reale Strukturen weisen jedoch stets, durch den Fertigungs- und Montageprozess bedingt, Abweichungen vom Sollzustand auf (Imperfektionen).
Temperaturfeldberechnungen können aus verschiedensten Gründen von Interesse sein, z.B. Beurteilung der Einhaltung von zulässigen Betriebstemperaturen, Abschätzung von Wärme- und Energieverlusten, Isothermenberechnungen, Untersuchung der Einflüsse aus temperaturbedingten Dehnungen und evtl. daraus resultierenden Spannungen oder entstehende Reibungswärme bei Kontaktproblemen usw.
Alle drei grundsätzlichen Fälle des Wärmetransports - Wärmeleitung (Konduktion), konvektiver Wärmeübergang und Strahlung (Radiation) - können sowohl im Zeitbereich als auch stationär berücksichtigt werden.
Komponenten und Bauteile weichen praktisch immer in irgendeiner Weise vom Idealzustand ab.
Besonders gravierend sind Fehler, die die Festigkeit beeinflussen und letztlich sogar zum Versagen führen.
Solche Fehler können dahingehend bewertet werden, ob sie während des bestimmungsgemäßen Betriebs oder auch bei seltenen
Extrembelastungen größer werden und zum Bruch des Bauteils führen.
Diese Bewertung erfolgt meist
mit den Konzepten der Bruchmechanik. Wobei als ungünstigste
Annahme unterstellt wird, dass es sich bei den Fehlern um Risse handelt. Aus den Bauteilbelastungen werden dann
Rissspitzenbeanspruchungen abgeleitet, die von der anliegenden Spannung und der Rissgröße abhängen.
Diese Beanspruchungen werden mit dem Risswiderstand verglichen (SIF oder J-Integral) bzw. mit entsprechenden
Risswachstumsgesetzen bewertet. Daraus können Entscheidungen über den Weiterbetrieb abgeleitet bzw. auch
Inspektionsintervalle festgelegt werden.


Anwendung von numerischen Berechnungs- und Simulationsmethoden - technische und ingenieurwissenschaftliche
Dienstleistungen mit verschiedensten Anforderungen

Consulting:
In-House Software:
User Experience:
Rapid Prototyping: